Лінійні регресії
Регресія – це метод визначення зв’язку між однією змінною (y) та іншими змінними (x).
У статистиці лінійна регресія — це підхід до моделювання лінійного відношення між y та x.
У машинному навчанні лінійна регресія — це контрольований алгоритм машинного навчання.
Діаграма розсіювання
Це діаграма розсіювання (з попереднього розділу):
Приклад
var xArray = [50,60,70,80,90,100,110,120,130,140,150];
var yArray = [7,8,8,9,9,9,10,11,14,14,15];
// Визначити дані
var data = [{
x:xArray,
y:yArray,
mode: "markers"
}];
// Визначити макет
var layout = {
xaxis: {range: [40, 160], title: "Квадратних метрів"},
yaxis: {range: [5, 16], title: "Ціна в мільйонах"},
title: "Ціни на житло в порівнянні з розміром"
};
Plotly.newPlot("myPlot", data, layout);
Спробуйте самі »
Прогнозування значень
Як ми можемо передбачити майбутні ціни на основі розрізнених даних вище?
- Використовуйте намальований від руки лінійний графік
- Моделюйте лінійну залежність
- Моделюйте лінійну регресію
Лінійні графіки
Це лінійний графік, який прогнозує ціни на основі найнижчої та найвищої ціни:
Приклад
var xArray = [50,60,70,80,90,100,110,120,130,140,150];
var yArray = [7,8,8,9,9,9,9,10,11,14,14,15];
var data = [
{x:xArray, y:yArray, mode:"markers"},
{x:[50,150], y:[7,15], mode:"line"}
];
var layout = {
xaxis: {range: [40, 160], title: "Квадратних метрів"},
yaxis: {range: [5, 16], title: "Ціни в мільйонах"},
title: "Ціни на житло в порівнянні з розміром"
};
Plotly.newPlot("myPlot", data, layout);
Спробуйте самі »
З попереднього розділу
Лінійний графік можна записати як y = ax + b
Де:
- y – це ціна, яку ми хочемо передбачити
- a – нахил лінії
- x – це вхідні значення
- b – перехоплення
Лінійні зв’язки
Ця модель передбачає ціни, використовуючи лінійну залежність між ціною та розміром:
Приклад
var xArray = [50,60,70,80,90,100,110,120,130,140,150];
var yArray = [7,8,8,9,9,9,10,11,14,14,15];
// Обчислити нахил
var xSum = xArray.reduce(function(a, b){return a + b;}, 0);
var ySum = yArray.reduce(function(a, b){return a + b;}, 0);
var slope = ySum / xSum;
// Генерувати значення
var xValues = [];
var yValues = [];
for (var x = 50; x <= 150; x += 1) {
xValues.push(x);
yValues.push(x * slope);
}
Спробуйте самі »
У наведеному вище прикладі нахил є обчисленим середнім значенням і перетином = 0.
Використання функції лінійної регресії
Ця модель передбачає ціни за допомогою функції лінійної регресії:
Приклад
var xArray = [50,60,70,80,90,100,110,120,130,140,150];
var yArray = [7,8,8,9,9,9,10,11,14,14,15];
// обчислити суми
var xSum=0, ySum=0 , xxSum=0, xySum=0;
var count = xArray.length;
for (var i = 0, len = count; i < count; i++) {
xSum += xArray[i];
ySum += yArray[i];
xxSum += xArray[i] * xArray[i];
xySum += xArray[i] * yArray[i];
}
// обчислити нахил і перетин
var slope = (count * xySum - xSum * ySum) / (count * xxSum - xSum * xSum);
var intercept = (ySum / count) - (slope * xSum) / count;
// генерувати значення
var xValues = [];
var yValues = [];
for (var x = 50; x <= 150; x += 1) {
xValues.push(x);
yValues.push(x * slope + intercept);
}
Спробуйте самі »
Поліноміальна регресія
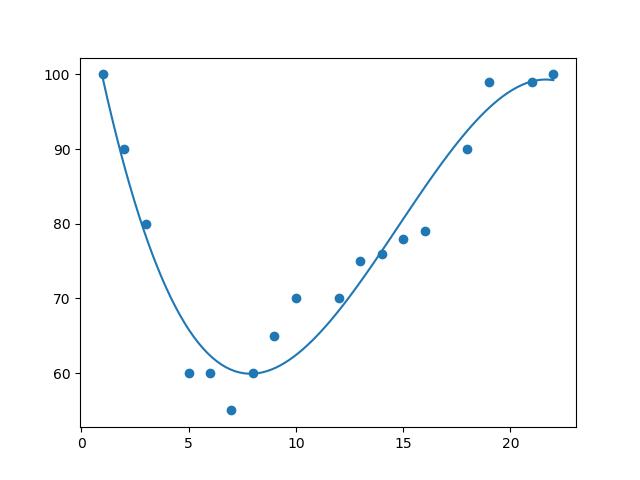
Якщо розсіяні точки даних не відповідають лінійній регресії (пряма лінія через точки), дані можуть відповідати поліноміальній регресії.
Поліноміальна регресія, як і лінійна регресія, використовує зв’язок між змінними x та y, щоб знайти найкращий спосіб провести лінію через точки даних.